■単に隠れているもの、本質的に感覚知覚できないもの
金子みすずの詩に「星とたんぽぽ」があります。昼間の星に対しても、タンポポの根に対しても見えぬけれどもあるんだよ
見えぬものでもあるんだよ
と語ります。
ただ、ここで「見えない」と言われているのは昼の星やタンポポの根であり、その対象が本質的に「見えない」からではなく、覆われているから見えないわけです。タンポポの根は土に覆われ、昼の星は光る空に覆われ見えないのです。ところが、物質界を離れますと本質的に「見えない」ものがあります。たとえば、私たちの魂の働き、つまり感情や思考は見えません。そして、アントロポゾフィーとかかわるなら避けては通れない霊的な世界(精神的な世界)も目では絶対に見えません。しかし確実に「見えぬけれどもある」のです。この「ある」を単に信じているのか、とりあえずそう考えているのか、実際に体験しているのか、では人生が大きく変わります。人は、霊界が存在することを体験しなくてはいけません。
■霊界を見るには
霊界と言ってもそこは大変に広く、誰にでも比較的簡単に見える部分と大変な修行を積まなければ見えない部分とがあります。簡単に見える部分であってもそれを一度しっかりと見てしまうと「霊界」を否定することはできなくなります。シュタイナーは霊界を否定する物質主義者を称して「ただの馬鹿」といったニュアンスのことを言っています。言い換えれば、ちゃんと考えれば霊界の存在は確認できるのです。そして、霊界の中で比較的簡単に見える「霊界お手ごろランド」が幾何学なのです。シュタイナー自身、子どもの頃に感覚界と霊界をつなぐ幾何学に大きな慰めを見出していた、と回想しています。■幾何学の定理
たとえば、円周角の定理というのがあります。円周上の一定の孤に立つ円周角はすべて等しい
という定理です。図の角a1、a2、a3等々が皆等しいというのです。

ここでしばらく、この定理の証明にお付き合いください。
■最も単純な場合
何らかの問題を考えていく上で「最も簡単な場合から考える」、という方法があります。特別にわかり易い場合から考えっていって、次第に難しい場合に移行していくのです。この方法をシュタイナーはピタゴラスの定理の教え方で示しています。直角三角形の中でも、事柄を考えやすい直角二等辺三角形(三角定規形)から教えていくのです。この円周角の問題では、円周角をなす直線の一方が、ちょうど円の半径になる場合が一番単純です。ですので、まずこの場合を考えてみましょう。
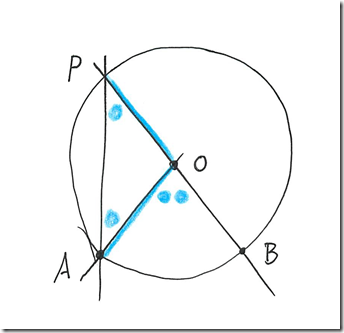
この図の中で幾何学的な法則を二つ用いることになります。一つは二等辺三角形の法則です。円の半径の長さはすべて等しいですから、
三角形AOPは二等辺三角形になり、その二つの底角は等しいここで使うもう一つの法則は、三角形の内角の和が一直線(180度)になるというものです。
(本来、この法則も証明される必要がありまが、ここでは省略です。)
中心角AOB+二等辺三角形の頂角AOP =180度
二等辺三角形の二つの底角(●)+二等辺三角形の頂角AOP = 180度ですから、
中心角AOB = 二等辺三角形の二つの底角の和となります。
二等辺三角形の底角は等しいですから、
中心角AOBの1/2 = 二等辺三角形の底角 = 円周角という関係が成り立ちます。つまりこの円周角は中心角の半分なのです。
図を見て、
●と●は等しく、●●はそれらの2倍(マルは本来、水色)という方が、理解は簡単でしょう。「△AOPで……」といった表現を追うだけで、けっこう集中力を使いますが、幾何学の本質的な部分は、実は、そんなに難しくないのです。
さて、次の段階は「どの円周角も中心角の半分」であることを示しますが、ここでは省略します。
■証明の核心
ここからが、重要です。ここでの証明の際に、私はフリーハンドの図を用いました。しかし人は、このような図であっても定理の証明を理解できます。つまり、目に見える図は、ある完全なる円について考えるきっかけでしかないのです。そして、その完全なる円はこの地上に目に見える形では存在しません。この事実をしっかり体験しますと、人は自分が霊界の住人であることを自覚するはずです。どう考えても、感覚知覚できない事柄(概念)を思考の中で知覚しているのですから。そして、その概念同士は思考世界(霊界)である特定の関係を保ちながら結びついているのです。たとえば、《二等辺三角形》と《等しい底角》という概念同士は一体です。
さて、思考が知覚であるなどと述べると「あれ?」と思われる人もいるでしょう。思考とは「自分で何か考え出す」ことと捉えられることが多いからです。しかし、それは事実ではありません。たとえば、数学の世界では「発見」はあっても「発明」はありません。ある定理を新たに見出すのであり、新たに作り出すのではないのです。
不完全な図を頼りに、霊界に存する完全な円を思考によって知覚し、そこにある事柄のつながりを見出しているのです。
この私たちが思考において、事情の概念同士の関係を知覚している、という点は、他の事柄でもまったく同じです。
■「コップは見えますか」
こんな質問を受けても、人は困惑するだけかもしれません。「コップなんて当たり前」と思っているからです。しかし、さらに質問を続けます。「コップの大きさはどれくらいですか」すると、コップが目に見える存在ではなくなることに気づくでしょう。もちろん、何らかの個別のコップは目に見えます。しかし、何をコップといい、何を言わないか、を吟味していくと、コップの概念が次第に明確になっていきます。
「コップの形はどうですか」
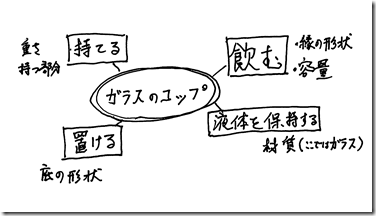
「コップとはガラスでできた器」とするなら、「それでは金魚鉢は?」と反論できます。ガラスでできた器であるにもかかわらず、コップとは思わないからです。こうしたことを考えていくと、コップという存在は、以下のような一種の概念コンプレックス(概念複合体)であると言えるでしょうし、これこそがコップのリアルな存在と思えるようになるはずです。そして、この概念コンプレックスから、水を飲むときのコップや、ビールを飲むときのコップなどを、状況に応じて発展させることができるのです。
■理念こそ、シュタイナーの出発点
シュタイナーの考え方は、常にこの概念複合体コンプレックス、言い換えると存在の理念的本質が出発点です。それゆえ、音楽では「音の本質」が、絵画では「色彩の本質」が出発点となりますし、教育では「成長する子どもの本質」を見極める必要が、どうしてもあるのです。表面ばかりを真似して、この本質について何も洞察していなければ、それはアントロポゾフィーとは全くの無関係です。
■霊界の諸性質
ここで、霊界の諸性質をまとめておきます。
- 永遠なる世界である
- 真と善からなる(美は含まれない)
- 空間的に物質界と分かれているわけではない
- とりあえずは思考によって、高次な領域には瞑想によって認識できる
- 霊界の下層部分の認識は難しくはない
- 霊界の下層部分には四大霊がある
0 件のコメント:
コメントを投稿